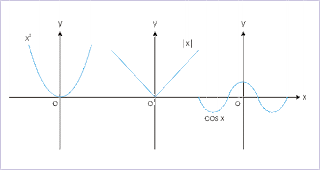
Even functions are functions where the left half of the plane, which would be in quadrant II, looks like the mirror image of the right half of the plane, which is in quadrant I. You can use the equation f(-x)=f(x)or x2. What it pretty much is is that for every X there is a -X in the domain.
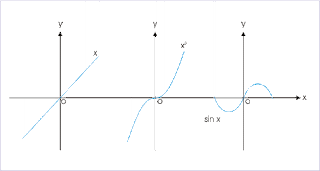
An odd function:
And odd function is where the upper right side of the plane, which is quadrant I, is symmetrical to the lower left side of the plane, which is quadrant III. It is symmetrical about the origin.An equation you can use for these type of functions are f(−x)=−f(x) or x3.
Very like clear to understand... like your graphs
ReplyDelete"What it pretty much is is that for every X there is a -X in the domain."
ReplyDeleteHm... never thought about this. This is true. =) HOwever, it does not make the function even. Also, what about reflection from quadrant 3 to quadrant 4 or vice versa?
For you odd explanation, what about functions like -x^3? That reflects from quadrant 2 to quadrant 4. Also, you're not explaining the actual equation but restating the definition of symmetry about the origin.