Transformations
With transformations i first look at what is inside the parenthesis. Whatever is inside the parenthesis will determine what whether you graph shifts to the left or to the right. If there is a negative/subtraction sign it will move to the right and if it is a positive/addition sign then it moves to the left. Then I look at what is outside the parenthesis. If there is a negative/subtraction sign it shifts down. If there is a positive/addition sign then you shift the graph up. It also depends on how many units come after the sign. One thing i try to remember is that for transformations , that Ms. Hwang commonly uses is that they are counter intuitive.
Trigonometry
I think trigonometry is basically centered around the unit circle. If you know all you radians, coordinates, and fractions then you are good. i try to remember that the sections go by 6, 4, 3, 2, then you flip them over on each side of the circle and for Quadrant II is one less than the denominator, Q.III is one more, and Q.IV is multiply by 2 subtract one. And i just remembered, for graphing, that cos(x) that it has a point at (0,1) and sin(x) is at the origin, and they look like speed bumps. For all the other ones i just remember that they have asymptotes .
What Confuses Me
Finding the periods and the domain and range for tan(x), csc(x), sec(x), cot(x), cos(x),and sin(x).
Saturday, November 21, 2009
Saturday, November 14, 2009
Lincoln Logs and Inverses
What I Understood
- To find the inverse of a function you switch the X and Y and there you go .
- I also learned that you don't have to graph the inverse of a function to see if the inverse is a function or not. You can determine if a function is on-to-one if you try the horizontal line test and if it has more that one point going through one of the lines then it is not one-to-one
- Symmetrical functions have a slope that is consistent .
- The inverse of (f) is (f^-1)
- The base of a log is usually always(oxymoron) 10 unless you have a different base there
What I Don't Understand
- When you have to use log or Ln. Like the equation (1.045)^t=2 and you have to solve for t, i don't get if i would have to use log or Ln for this equation.
- I don't understand how to solve an equation when there is two X's.
- I also don't understand when you have to find the inverse of an equation that is a fraction .
- I don't understand how to graph logs
- I don't get how to solve f(g(x))=x but g(x) is not the inverse of x !!!! Like what does that even mean !!!! that problem confused the hell out of me :T
And it helps that I sit next to Ivan S. because he helps me out a lot when i don't get it. Thanks Ivan =) ....
Saturday, November 7, 2009
Even and Odd functions
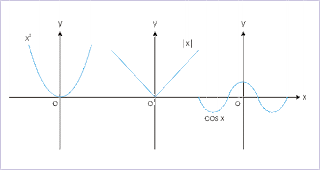
An even function :
Even functions are functions where the left half of the plane, which would be in quadrant II, looks like the mirror image of the right half of the plane, which is in quadrant I. You can use the equation f(-x)=f(x)or x2. What it pretty much is is that for every X there is a -X in the domain.
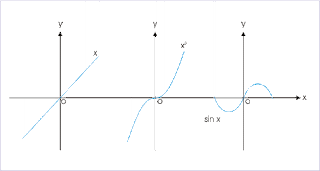
An odd function:
And odd function is where the upper right side of the plane, which is quadrant I, is symmetrical to the lower left side of the plane, which is quadrant III. It is symmetrical about the origin.An equation you can use for these type of functions are f(−x)=−f(x) or x3.
Even functions are functions where the left half of the plane, which would be in quadrant II, looks like the mirror image of the right half of the plane, which is in quadrant I. You can use the equation f(-x)=f(x)or x2. What it pretty much is is that for every X there is a -X in the domain.

An odd function:
And odd function is where the upper right side of the plane, which is quadrant I, is symmetrical to the lower left side of the plane, which is quadrant III. It is symmetrical about the origin.An equation you can use for these type of functions are f(−x)=−f(x) or x3.

Subscribe to:
Comments (Atom)